트리의 특징
트리에서는 어떠한 두 정점을 고르더라도 두 정점 사이를 연결하는 경로는 유일하게 결정된다는 특징이 있습니다. 또한, 트리의 모든 정점은 트리의 root 역할을 수행할 수 있습니다.
각 간선에 가중치가 있는 트리 정보가 주어졌을 때, 트리의 지름이란
모든 정점 쌍에 대한 거리 중 가장 긴 경로의 길이
를 말합니다.
트리의 지름을 찾는 알고리즘
트리의 지름을 가장 쉽게 구하는 방법은 다음과 같습니다.
- 아무 정점이나 잡고 시작해 DFS를 이용해 시작점으로부터 가장 먼 정점을 구합니다. 거리가 동일한 정점이 여러 개라면 아무 정점이나 골라도 상관없습니다.
- DFS를 통해 동일한 방식으로 위에서 구한 정점을 시작점으로 하였을 때, 가장 먼 정점을 구합니다.
- 이때 구해진 거리가 트리의 지름이 됩니다.
예로 아래 그림에서 트리의 지름을 구해보겠습니다.

1번 정점을 시작으로 DFS를 통해 가장 먼 정점을 구합니다. 가장 먼 정점을 7번 정점이 됩니다.

이제 7번 정점을 시작으로 가장 먼 정점을 구합니다. 가장 먼 정점은 5번 정점이 되며, 따라서 7번 정점과 5번 정점으로 이루어져 있는 경로의 길이가 트리의 지름이 됩니다.
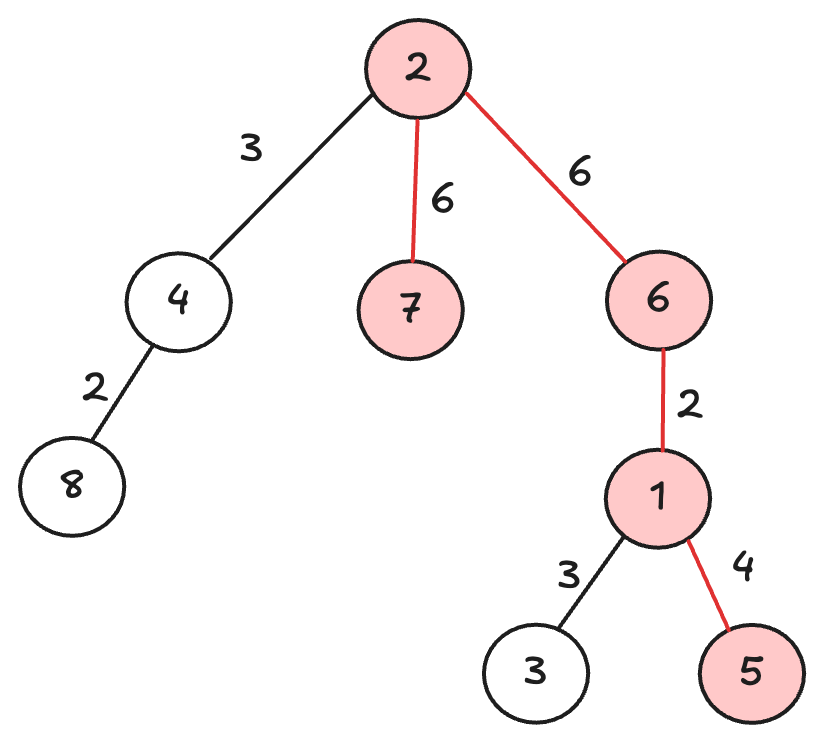
따라서 트리의 지름을 구하는 알고리즘의 시간복잡도는 $O(N)$이 됩니다.
코드
입력이 다음과 같이 주어질 때,
첫 번째 줄에 트리의 정점의 개수 N이 주어집니다.
그 다음 줄부터 N - 1 개의 줄에 걸쳐, 트리의 각 간선이 연결하는 두 정점의 번호와 그 간선의 길이가 공백으로 구분되어 주어집니다.
트리의 지름을 구하는 코드는 다음과 같습니다.
import java.util.Scanner;
import java.util.ArrayList;
class Pair {
int num, dist;
public Pair(int num, int dist) {
this.num = num;
this.dist = dist;
}
}
public class Main {
public static final int MAX_N = 100000;
// 변수 선언:
public static int n;
public static ArrayList<Pair>[] edges = new ArrayList[MAX_N + 1];
public static boolean[] visited = new boolean[MAX_N + 1];
public static int[] dist = new int[MAX_N + 1];
// DFS를 통해 연결된 모든 정점을 순회합니다.
// 동시에 시작점으로부터의 거리를 같이 계산해줍니다.
public static void dfs(int x, int totalDist) {
// 노드 x에 연결된 간선을 살펴봅니다.
for(int i = 0; i < edges[x].size(); i++) {
int y = edges[x].get(i).num;
int d = edges[x].get(i).dist;
// 아직 방문해본적이 없는 노드인 경우에만 진행합니다.
if(!visited[y]) {
visited[y] = true;
dist[y] = totalDist + d;
dfs(y, totalDist + d);
}
}
}
// 정점 x로부터 가장 멀리 있는 정점 정보를 찾아줍니다.
public static Pair FindLargestVertex(int x) {
// visited, dist 값을 초기화해줍니다.
for(int i = 1; i <= n; i++) {
visited[i] = false;
dist[i] = 0;
}
// 정점 x를 시작으로 하는 DFS를 진행합니다.
visited[x] = true;
dist[x] = 0;
dfs(x, 0);
// 정점 x로부터 가장 멀리 떨어진 정점 정보를 찾습니다.
int farthestDist = -1;
int farthestVertex = -1;
for(int i = 1; i <= n; i++) {
if(dist[i] > farthestDist) {
farthestDist = dist[i];
farthestVertex = i;
}
}
// 가장 멀리 떨어진 정점 번호와 그때의 거리를 반환합니다.
return new Pair(farthestVertex, farthestDist);
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
// 입력:
n = sc.nextInt();
for(int i = 1; i <= n; i++)
edges[i] = new ArrayList<>();
// n - 1개의 간선 정보를 입력받습니다.
for(int i = 1; i <= n - 1; i++) {
int x = sc.nextInt();
int y = sc.nextInt();
int d = sc.nextInt();
// 간선 정보를 인접리스트에 넣어줍니다.
edges[x].add(new Pair(y, d));
edges[y].add(new Pair(x, d));
}
// 1번 정점으로부터 가장 멀리 있는 정점 정보를 찾습니다.
int fVertex = FindLargestVertex(1).num;
// farthest vertex로부터 가장 멀리 있는 정점 정보를 찾습니다.
// 이때의 거리가 지름이 됩니다.
int diameter = FindLargestVertex(fVertex).dist;
System.out.print(diameter);
}
}'알고리즘 > 알고리즘' 카테고리의 다른 글
| [Algorithm] Lower Bound & Upper Bound (2) | 2024.12.17 |
|---|---|
| [Algorithm] 위상 정렬(Topological Sort) (1) | 2023.04.14 |
| [Algorithm] 분할 정복 (0) | 2022.08.25 |
| [Algorithm] BFS : 너비 우선 탐색(Java) (0) | 2022.08.02 |
| [Algorithm] 플로이드-워셜(Floyd-Warshall) 알고리즘 (0) | 2022.07.06 |

