📂 위상 정렬이란?
DAG(Directed Acycle Graph : 비순환 방향 그래프)에서 정점들을 선형으로 정렬하는 것을 말한다.
DAG는 말 그대로, 사이클이 존재하지 않으면서 방향성을 가진 그래프이다.
이해하기 쉽게 그래프를 통해 알아보자.

다음과 같은 DAG가 있다고 가정해보자.
정점들의 위상에 맞게 정렬하는 것이므로, 간선의 방향성에 맞게(방향성을 조건으로 삼아서) 정점들의 번호를 선형으로 저장하는 것이다.
위 그래프를 예로 본다면, 다음과 같이 정렬될 수 있다.
| 1 | 3 | 5 | 4 | 2 | 6 |
이 정렬 조건에서 무엇이 만족되어야 하냐면, 모든 간선마다 1에서 4로 향하는 간선이 있다면 정렬 조건에서 1번이 4번보다 먼저 나타나야 한다. 3번에서 6번으로 바로가는 간선은 없지만, 2번으로 가는 간선이 있으므로 3번이 2번보다 먼저 나타나야 하고 이 2번은 2번에서 6번으로 가는 간선이 있기 때문에, 6번보다 먼저 나타나게 된다.
즉, 간선 하나하나마다 어떤 정점이 어떤 정점보다 먼저 와야 한다는 것을 의미한다.
모든 간선이 조건을 만족하도록 정점들을 나열하는 것을 위상 정렬이라고 한다.
📂 동작 방법
위상 정렬을 적용하는 가장 쉬운 방법은 "제일 먼저 올 수 있는 정점은?" 을 생각해보는 것이다.
제일 먼저 올 수 있는 정점? 이란 질문에 대한 대답은 "들어오는 간선이 없는 정점" 즉, Indegree가 0인 정점이다.
어떤 정점 x에 들어오는 간선 y가 있다고 생각하면, 위상 정렬에서 y가 x보다 먼저 나타나야 할 것이다. 그렇다면 x가 제일 앞에 올 수 없을 것이다.
제일 먼저 올 수 있는 정점 즉, Indegree가 0인 정점들을 먼저 담아준다. 이들 중 아무거나 골라서 가장 앞에 정렬시킨다. 그리고 그래프에서 그 정점을 지워버린다. 그 후 남아 있는 그래프에 대해 정렬한 결과를 그 뒤에 붙여주면 될 것이다.
예시를 보며 살펴 보자. 다음과 같은 그래프가 있다.
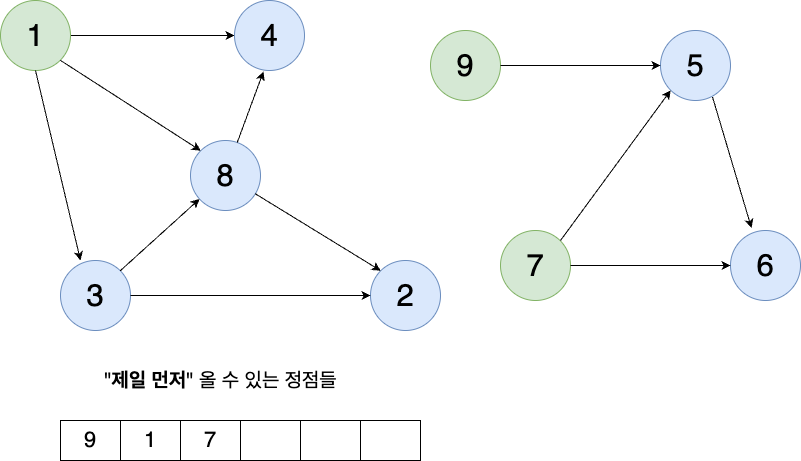
이 중에서 9번을 먼저 꺼내보자. 9를 정렬하고 그래프에서 삭제시킨다. 결과는 다음과 같다.
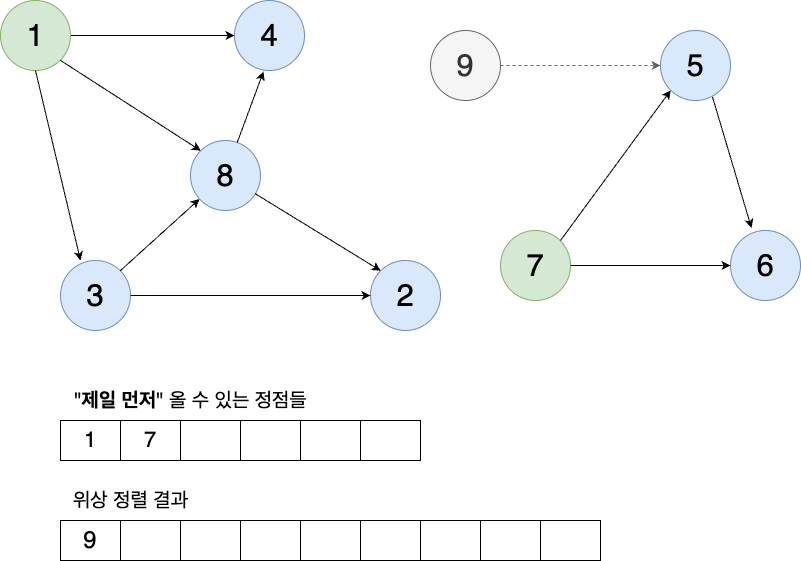
9가 삭제됨으로 인해 새롭게 "제일 먼저" 올 수 있는 정점이 있는지를 보자. 5번의 경우, Indegree가 7번으로 존재하기 때문에 불가능하다. 따라서 그냥 넘어가자!
다음으로는 1번을 꺼내보자.
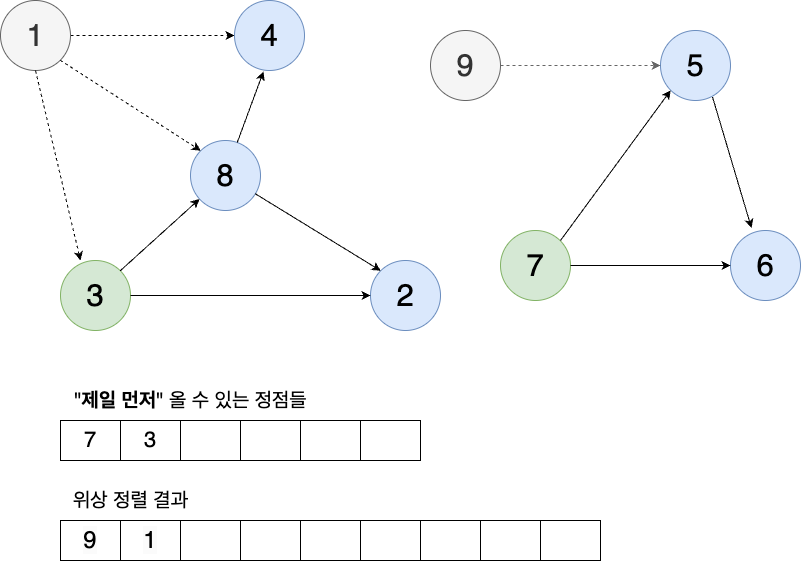
1번을 꺼내고 그래프에서 삭제시켰다. 그렇다면 1번에서 갈 수 있는 3, 8, 4번에 대한 정점도 사라지게 될 것이다. 이렇게 되면 3번 정점은 들어오는 정점이 사라진다. 즉, Indegree가 0이 된다. 3번 정점은 현재 남아있는 2, 4, 5, 6, 7, 8번 정점에 대해 가장 앞에 올 수 있는 후보가 되기 때문에 "제일 먼저" 올 수 있는 정점들에 추가시켜 준다.
이 과정들을 계속 반복하여 위상 정렬의 결과를 다음과 같이 얻을 수 있다.
| 9 | 1 | 7 | 3 | 5 | 8 | 6 | 4 | 2 |
📂 정리 & 구현
위 동작 방법을 정리해보면 다음과 같다.
- 정점들의 Indegree, Indeg[1...N] 계산하기
- 들어오는 간선이 0개인(Indeg[i] == 0) 정점들을 찾아서 자료구조 D에 넣기
- D가 빌 때까지(Empty)
- D에서 원소 X를 꺼내서 "정렬"시키기
- Graph에서 정점 X "제거"하기
- "새롭게 정렬 가능한 점"을 찾아서 D에 넣기
2, 3번에서 "제일 먼저" 올 수 있는 정점을 저장하는 자료구조 D에서 필요한 연산은
- 원소를 추가하기
- 원소를 꺼내기
이 두 가지 밖에 없다. 따라서 이 두 연산을 빠르게 O(1)에 수행시켜주는 Queue 자료구조를 이용한다.
위 순서를 토대로 구현을 해보면 다음과 같이 표현될 수 있다.
Queue<Integer> queue = new LinkedList<>();
// 처음에 시작할 정점들 넣기
for(int i=1;i<=N;i++){
if(indeg[i] == 0)
queue.add(i);
}
while(!queue.isEmpty()){
// 정점 꺼내기
int x = queue.poll();
// 정렬 결과를 넣기
result.add(x);
// x와 연결되어 있는 모든 정점 y에 대하여
for(int y : graph.get(x)){
// y의 indegree를 1 감소 -> x 정점을 지우는 역할(연결 끊기)
indeg[y]--;
// 만약 y에 들어오는 정점이 없다면, y를 큐에 넣기
if(indeg[y] == 0)
queue.add(y);
}
}
'알고리즘 > 알고리즘' 카테고리의 다른 글
| [Algorithm] Lower Bound & Upper Bound (2) | 2024.12.17 |
|---|---|
| [Algorithm] 트리의 지름 (0) | 2024.12.06 |
| [Algorithm] 분할 정복 (0) | 2022.08.25 |
| [Algorithm] BFS : 너비 우선 탐색(Java) (0) | 2022.08.02 |
| [Algorithm] 플로이드-워셜(Floyd-Warshall) 알고리즘 (0) | 2022.07.06 |

