이번 포스팅에서는 어떻게 좋은 데이터베이스를 설계할 것인가에 대한 이론적인 해결 방안에 대해 알아보자.
다음은 잘못 설계된 데이터베이스의 예이다.
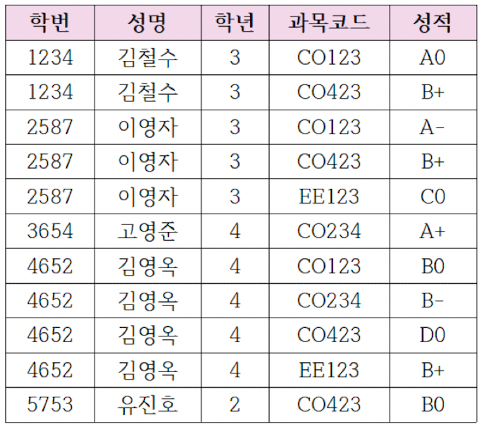
왜냐하면 같은 학번이 나타날 때마다 학년 애트리뷰트 값도 똑같이 중복적으로 나타나기 때문이다. 위 테이블과 같이 잘못 설계된 데이터베이스에서는 다음과 같은 삭제, 삽입, 갱신 이상이 발생된다. 이러한 이상(Anomaly) 현상에 대해 예를 들어 살펴보자.
🏷 삭제 이상(Deletion anomaly)
위 테이블에서 학번 3654 '고영준' 학생이 과목 'CO234'의 등록을 취소할 때는 DB에서 학번 3654인 튜플을 삭제하면 된다. 이때 3654번 학생의 학년이 4라는 정보가 이 튜플에만 존재해 있다. 따라서 이 튜플을 삭제하게 되면 3654번 학생이 4학년이라는 정보도 함께 삭제되어 이 정보는 더 이상 DB에서 찾을 수 없게 된다. 이처럼 연쇄 삭제(Triggered deletion)에 의해 정보가 영원히 손실되는 현상이 일어난다.
🏷 삽입 이상(Insertion anomaly)
테이블에 학번이 7654이고 학년이 3인 학생이 복학해서 본인 정보를 입력하려고 할 때 삽입할 수가 없다. 왜냐하면 이 테이블은 학번과 과목 코드가 기본키이므로 어떤 과목을 등록하지 않는 한 삽입이 불가능하다(PK는 NULL 값을 가질 수 없기 때문이다). 이 학생은 복학해서 아직 과목 신청을 하지 않았기 때문에 과목 정보가 없는데도 불구하고 학생 명부에 입력할 수 없는 이상 현상이 발생된다.
🏷 갱신 이상(Update anomaly)
학번 4652인 학생의 학년이 잘못 기재되어 4에서 3으로 변경하려고 할 때 학번 4652에 대한 4개의 튜플에 대해 모두 변경해야만 데이터베이스가 정확하게 된다. 하지만 만일 하나라도 4가 그대로 남아 있다면 데이터 정확성이 무너지게 된다. 즉, 중복된 데이터에 대해 일부만 갱신됨으로써 정보의 모순성(Inconsistency)이 발생된다.
이러한 문제를 해결하기 위한 방법은 애트리뷰트들 간의 종속성을 분석해서 하나의 릴레이션에는 하나의 종속성만 표현되도록 테이블을 분해(Decomposition)하는 것이다.
위의 릴레이션에서는 학번에 대해 성명과 학년이 종속 관계를 나타내고, 학번과 과목 코드에 대해서 성적이 종속 관계를 나타내고 있다. 이 종속 관계에 따라 두 개의 릴레이션으로 분해한다면 그 결과는 다음과 같다.
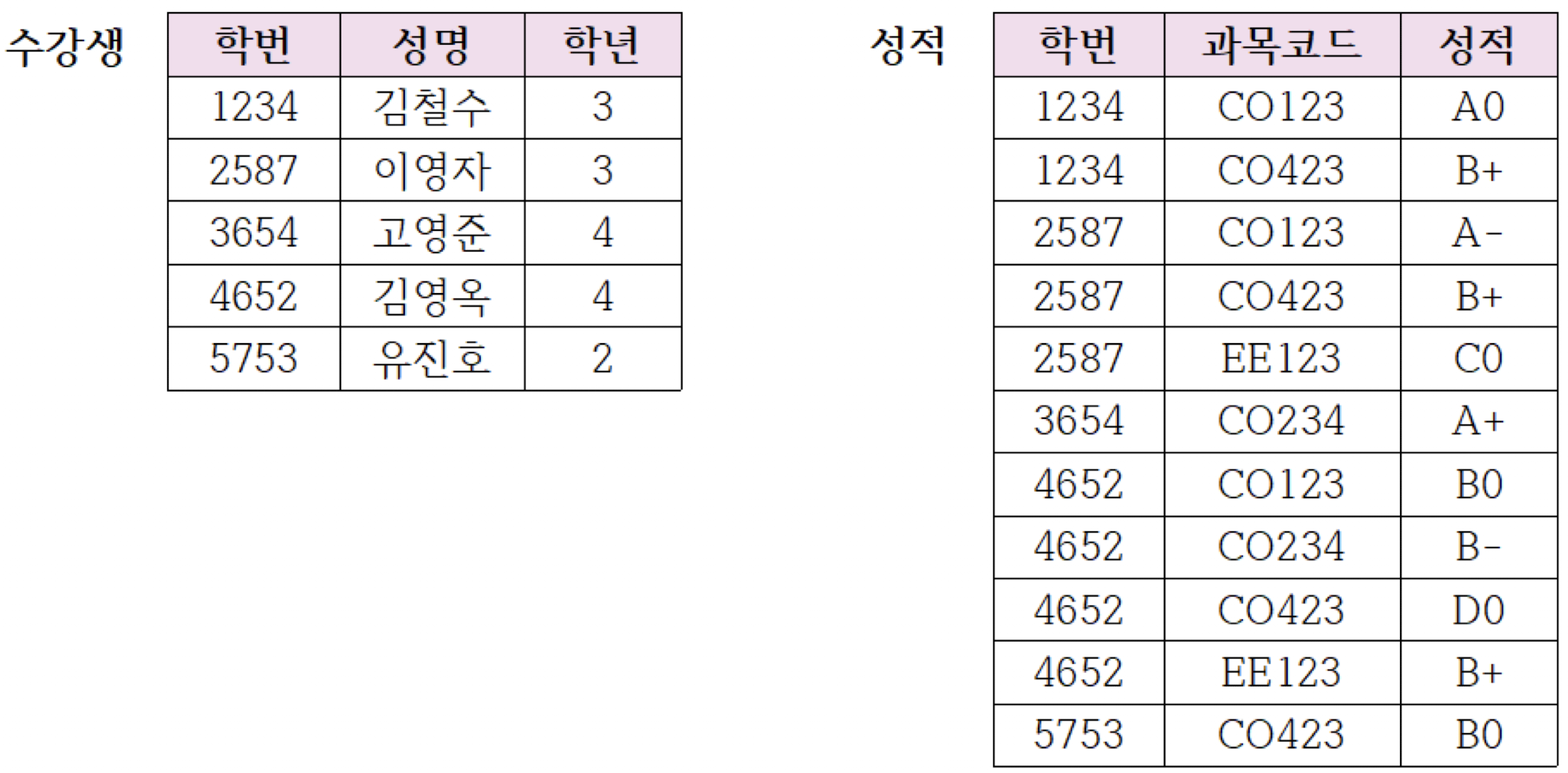
이처럼 하나의 릴레이션을 좀 더 단순하고 바람직한 구조를 갖는 두 개 이상의 릴레이션으로 분해하는 과정을 정규화(Normalization)라고 한다.
📂 함수 종속성
정규화 과정에서 가장 중요한 작업 중 하나가 함수 종속성을 찾아내는 것이다. 어떤 애트리뷰트 값은 다른 애트리뷰트의 값을 고유하게 결정할 수 있다. 예를 들어, 학생 릴레이션에서는 학번은 성명, 학과와 전화번호를 고유하게 결정한다.
즉, 결정자는
주어진 릴레이션에서 다른 애트리뷰트들을 결정하는 하나 이상의 애트리뷰트
를 의미한다. 학생 릴레이션에서는 학번이 성명, 학과, 전화번호의 결정자이다.
따라서, 만약 애트리뷰트 A가 애트리뷰트 B의 결정자이면 B가 A에 함수 종속(FD:Functional Dependency)된다고 말할 수 있다.
이를 기호로 표시하면 A → B 가 된다. 학생 릴레이션의 경우 '학번→(성명, 학과, 전화번호)'와 같이 표현된다.
함수 종속 다이어그램(FD diagram)은 한 릴레이션에서 애트리뷰트들 간의 함수 종속 관계를 쉽게 이해하기 위해 도식으로 표현한 것을 말한다. 위의 릴레이션을 함수 종속 다이어그램으로 표현하면 다음과 같다. 여기서 PK는 [학번, 과목 코드]이다.
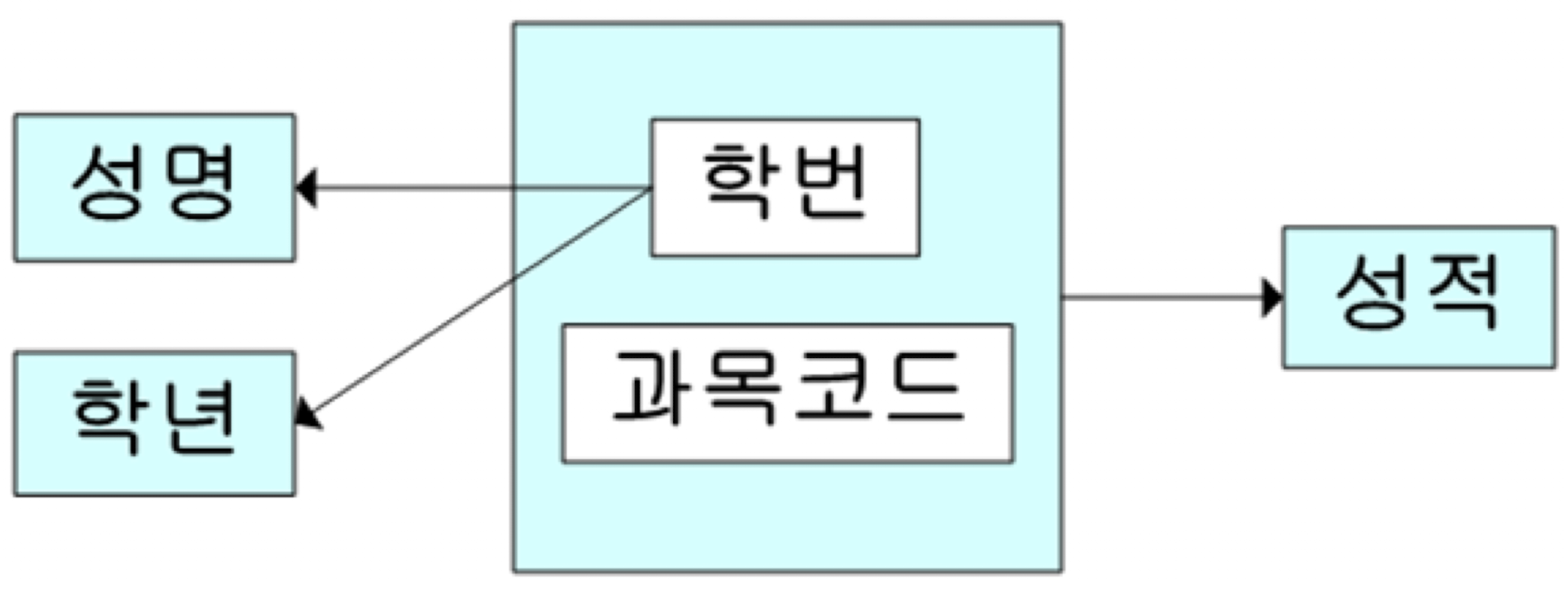
이 그림을 살펴보면 다음과 같이 3개의 함수 종속 관계가 존재한다.
- [학번, 과목 코드] → 성적
- 학번 → 성명
- 학번 → 학년
또한, 성적은 [학번, 과목 코드]에 완전 함수 종속(Full functional dependency)되었다고 하고, 성명과 학년은 학번에 완전 함수 종속되었다고 할 수 있다. 하지만, 성명과 학년은 [학번, 과목 코드]에 부분 함수 종속(Partial functional dependency)되었다고 한다.
📂 제1 정규형

위 릴레이션은 DBMS의 릴레이션이 될 수 없는 정규화되지 않은 비정규 릴레이션이다.
이 테이블에서 기본키는 [학번, 과목 코드]가 될 수 있고, 학번과 과목 코드의 조합으로 학생이 등록한 과목의 성적을 식별할 수 있다. 한 학생은 한 지도교수, 한 학과에만 속하고 각 지도교수도 한 학과에만 속한다.
비정규 릴레이션으로부터 제1 정규형(1NF: First Normal Form)을 만들어보자.
만약 릴레이션 R에 속한 모든 도메인이 원자 값만으로 되어 있다면 이 릴레이션은 제1 정규형이라 할 수 있다. 따라서 위의 비정규 릴레이션에서 아래와 같이 학번, 성명, 학과, 지도 교수 애트리뷰트에 보이는 빈칸을 모두 채운다면 도메인이 원자 값만으로 구성되었다고 할 수 있고 이 테이블은 제1 정규형에 속한다고 할 수 있다.
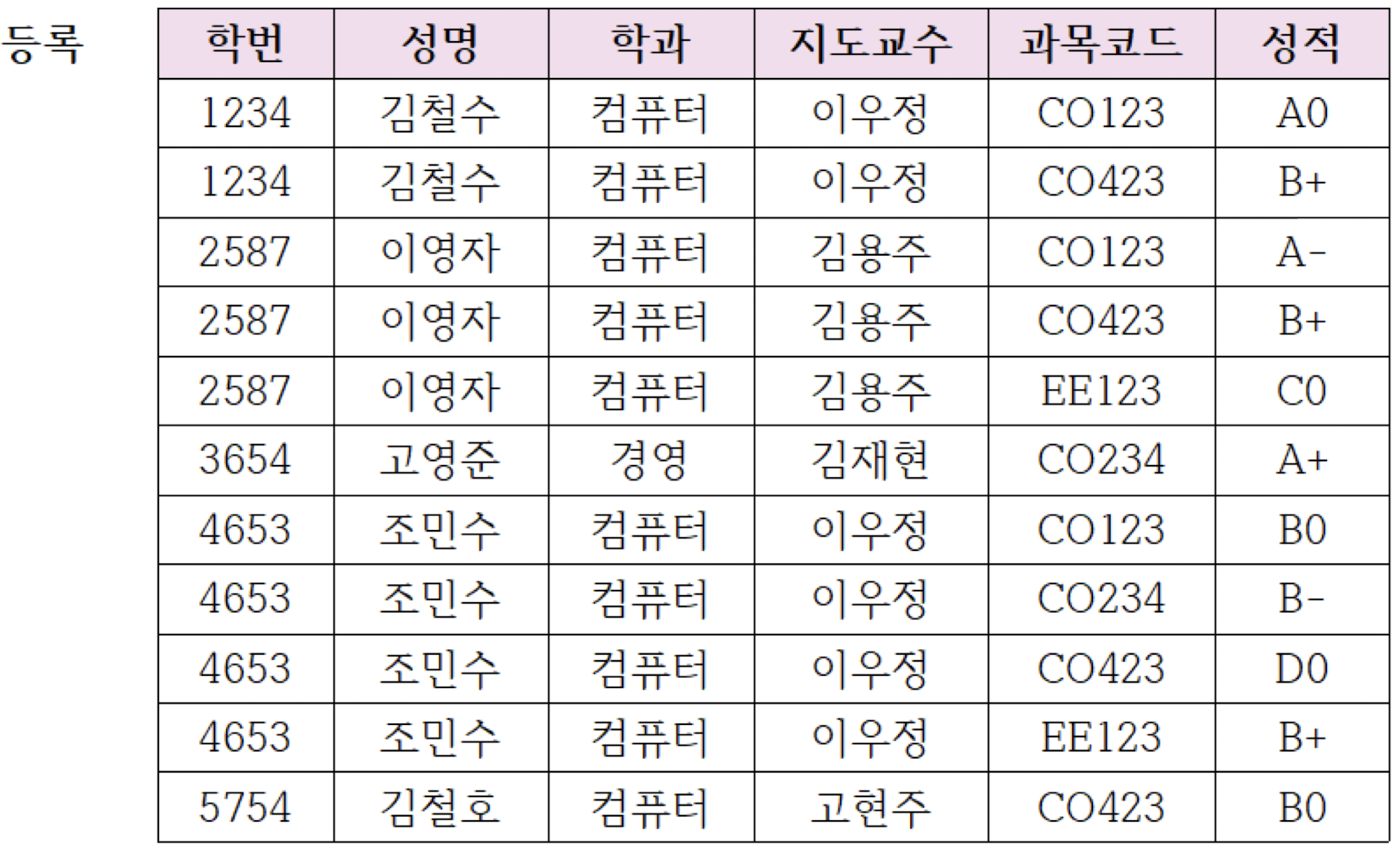
하지만, 위 테이블에 대한 함수 종속 다이어그램을 그려보면 문제점이 발생한다.
성적은 완전하게 보이지만, 성명, 지도교수, 학과의 화살표는 PK의 사각형에 겹쳐 있는 것을 볼 수 있다. 즉, 아직 불완전하다고 할 수 있다. 이 등록 릴레이션에서 발생될 수 있는 이상 현상들은 다음과 같다.
🏷 삽입 이상
학번 7654인 학생이 지도교수를 '김용주'로 선정하여 새로 입력시키려고 하는 경우를 보자. 이 경우, 학생은 어떤 과목을 등록하지 않는 한 자신의 튜플을 이 테이블에 삽입할 수 없다. PK인 과목 코드가 NULL이 될 수 없기 때문이다.
🏷 삭제 이상
학번 3654인 학생이 과목 'CO234'를 등록 취소하고자 할 때, 그 튜플을 삭제하면 된다. 하지만 이 튜플이 삭제되는 경우 지도교수 '김재현'이 속한 '경영'과 정보까지 삭제되어 더 이상 김재현의 학과 정보는 찾아볼 수 없게 된다.
🏷 갱신 이상
학번 4653인 학생이 지도교수를 '고현주'로 변경하고자 할 때, 학번이 4653인 4개의 튜플 모두에 대해 변경하지 않는다면 데이터 불일치 문제가 발생할 수 있다.
1NF에서 이상 현상의 원인은 키가 아닌 애트리뷰트들이 PK에 완전 함수 종속되지 못하고 부분 함수 종속되기 때문이다.
이에 대한 해결책은 위 다이어그램에서 아직 완전하지 못한 학번, 성명, 학과, 지도교수 부분을 따로 분리하여 두 개의 릴레이션으로 분할함으로써 해결할 수 있다.
즉, 부분 함수 종속을 제거하면 제2 정규형(2NF)이 된다.
📂 제2 정규형(2NF)
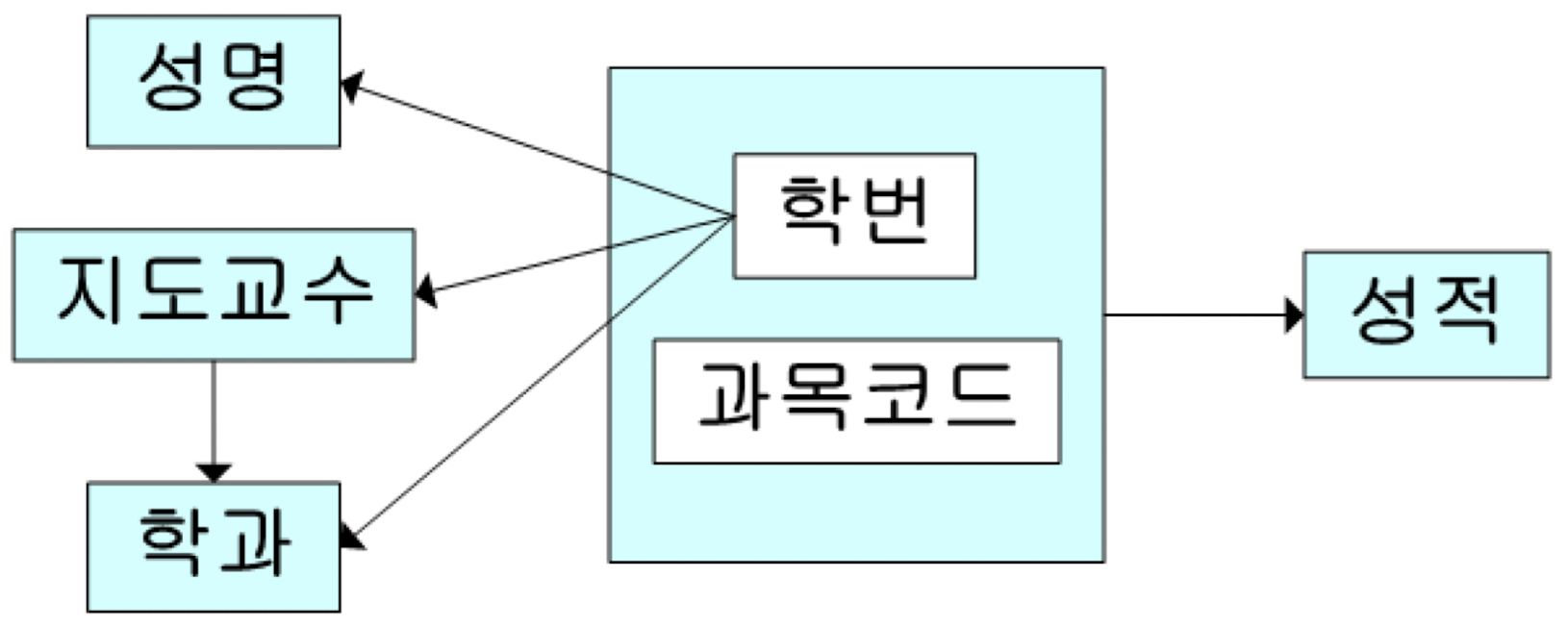
위 다이어그램의 부분 함수 종속을 제거한 후 함수 종속 다이어그램을 다시 그리면 다음과 같다.

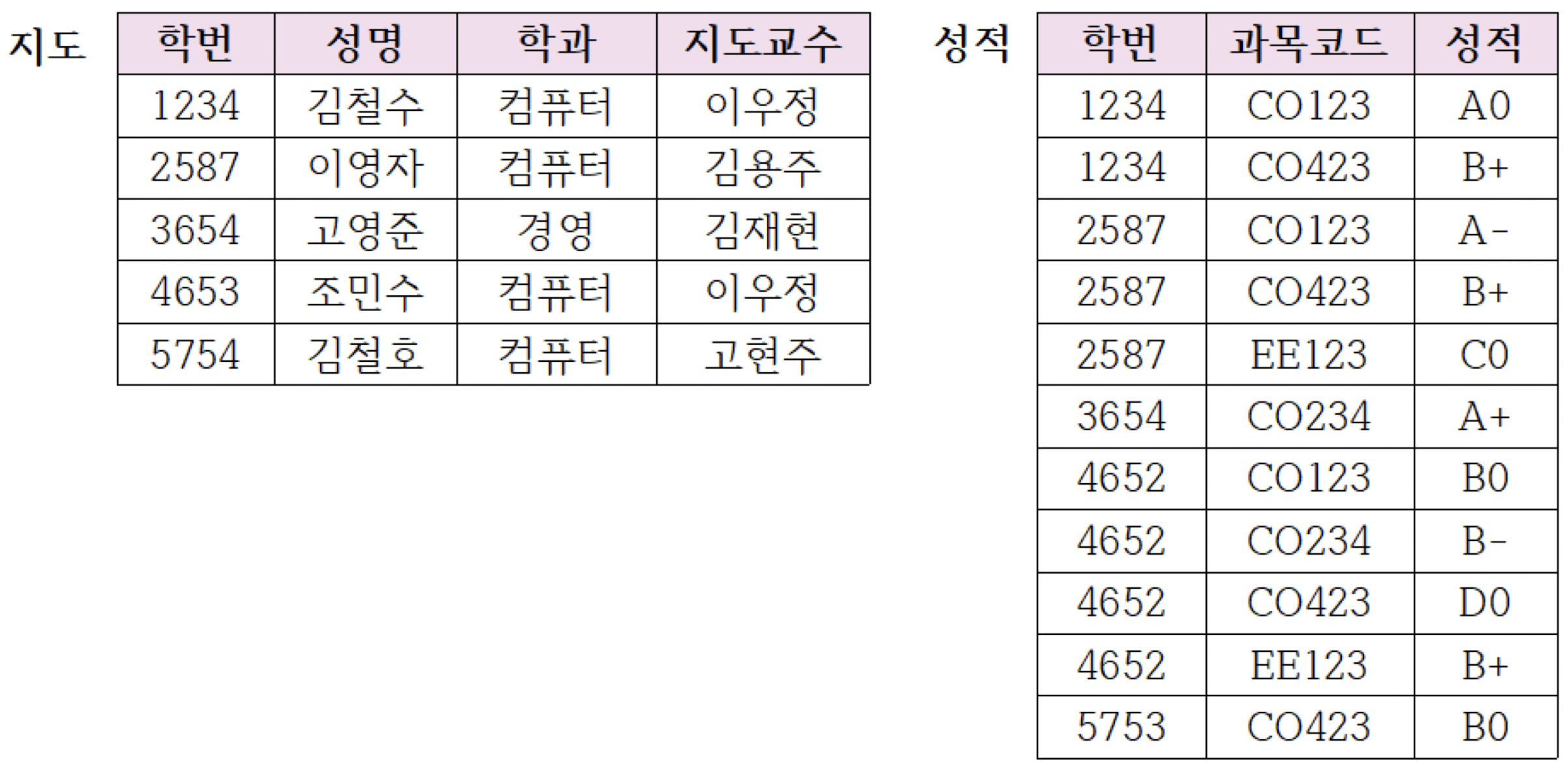
이 다이어그램으로부터 지도(학번, 성명, 학과, 지도교수)와 성적(학번, 과목 코드, 성적) 릴레이션을 만들고 테이블 내 나타나는 중복 데이터들을 제거하면 아래와 같은 제2 정규형을 만들 수 있다.
이제 이 다이어그램을 살펴보면 성적은 완전하게 보인다. 그러나 학번, 성명, 지도교수, 학과 관계는 종속 관계가 한 가지로 명확하게 정의되지 못하고 조금 불완전한 관계를 보이고 있다.
지도 릴레이션에서 발생할 수 있는 이상 현상을 살펴보자.
🏷 삽입 이상
지도교수 '강성화'가 '컴퓨터'과에 속한다는 사실을 삽입할 수 없다. 이 테이블의 PK는 학번인데 지도받는 학생이 아직 없는 NULL이기 때문이다.
🏷 삭제 이상
학번 2587인 학생이 지도교수와의 관계를 취소하고 할 때 이 튜플을 삭제하면 된다. 하지만 그렇게 되면 지도교수가 속한 학과 정보까지도 삭제되는 이상 현상이 발생한다.
🏷 갱신 이상
지도교수 '이우정'의 소속을 '컴퓨터'과에서 '전자'과로 변경하고자 한다면 1234, 4653 학번 2개의 튜플을 모두 변경해야 한다. 그렇지 못하면 데이터 불일치 모순이 발생한다.
2NF에서 이상 현상이 발생되는 이유는 두 개의 상이한 정보를 하나의 릴레이션으로 혼합해서 표현하려고 하는 데서 온다.
한 릴레이션의 애트리뷰트 A, B, C가 주어졌을 때, A가 PK라면 키의 정의에 따라 A→B, A→C가 성립한다. 그런데 C가 A 이외에도 B에도 함수 종속한다면 C는 A에서 B를 거쳐서 이행적으로도 종속한다. 이를 C는 A에 이행적 함수 종속(Transitive FD)된다 한다.
따라서 2NF 릴레이션의 이상 현상을 해결하기 위해서는 이러한 이행적 함수 종속을 제거해 두 개의 릴레이션으로 분해하는 것이다.
📂 제3 정규형
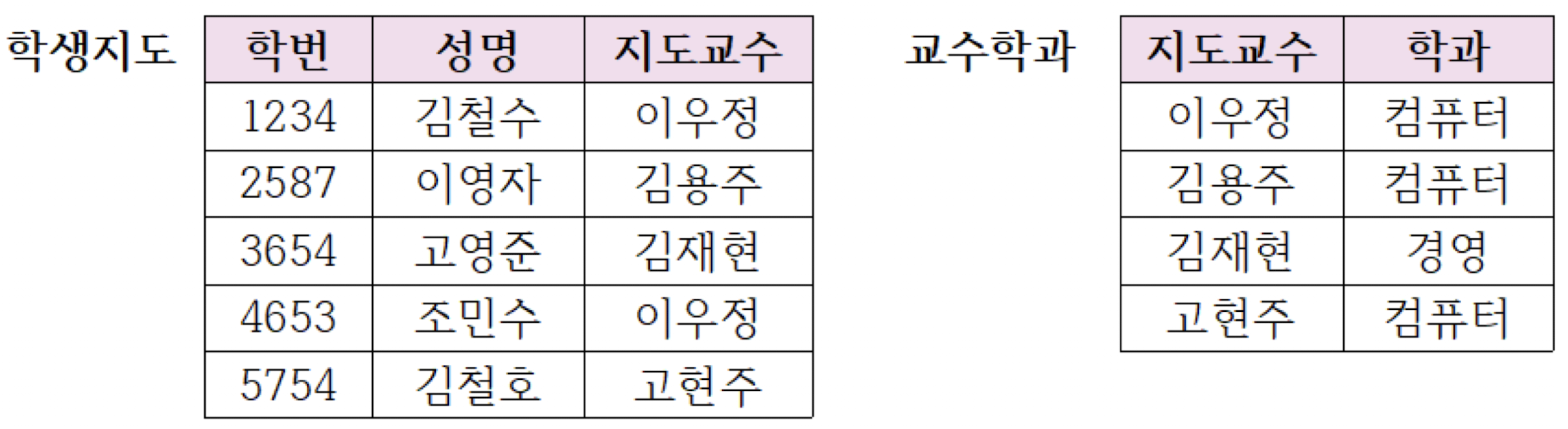
다시 학번, 성명, 학과, 지도교수를 학번, 성명, 지도교수와 지도교수, 학과로 분해한 다이어그램은 다음과 같다.
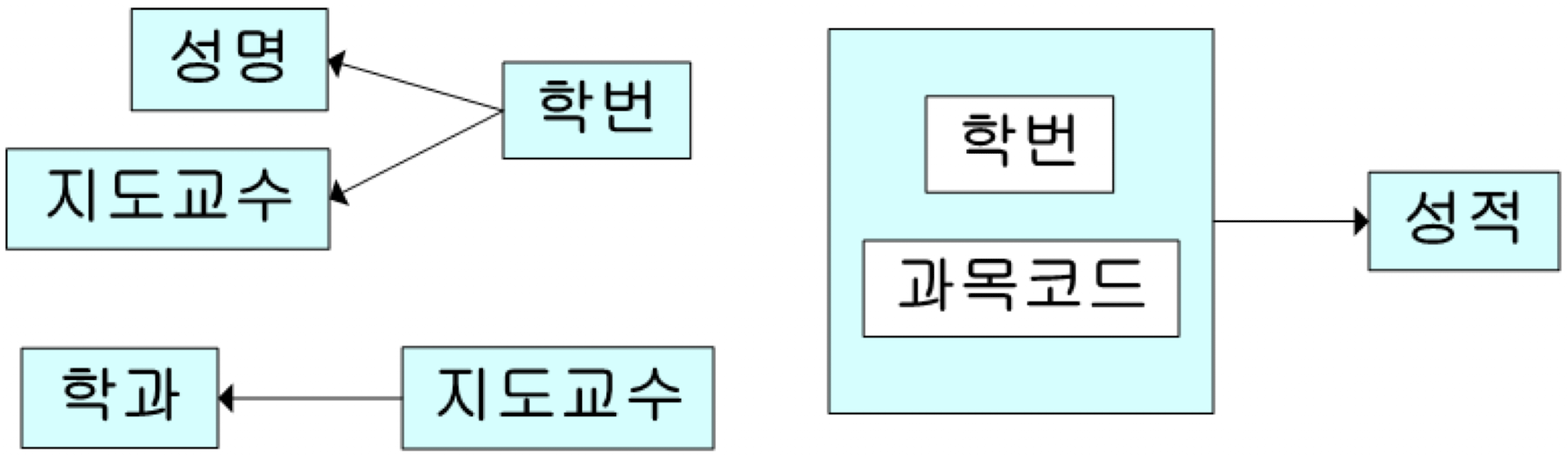
이와 같이 이행적 함수 종속을 제거한 두 개의 릴레이션과 성적 릴레이션은 이제 비로써 제3 정규형(3NF)이 되었다고 할 수 있다. 일반적으로 DB에서 3NF는 거의 완벽한 수준이라고 말할 수 있으며 데이터베이스 설계의 목표가 3NF를 만드는 것이라 할 수 있다.
📂 보이스/코드 정규형
DB에서 3NF는 거의 완벽한 설계라 할 수 있지만, 간혹 문제점이 있는 예가 있다. 이러한 예를 보이스/코드 정규형(BCNF: Boyce/Codd Normal Form)이라 한다.
예를 통해 살펴보자.
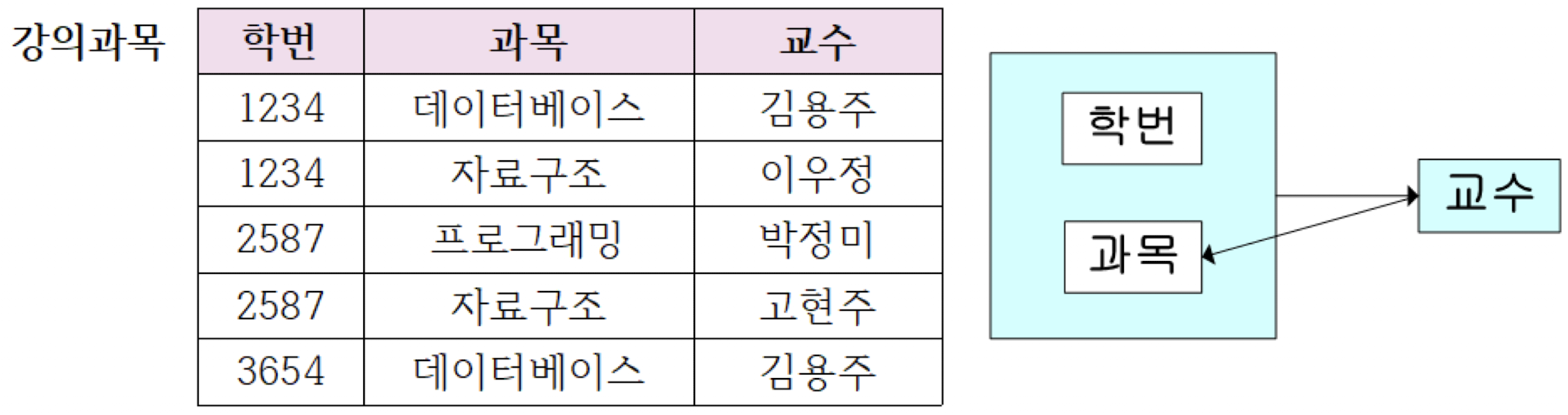
위와 같은 강의 과목 릴레이션에서 제약 조건이 다음과 같다고 가정해보자.
- 한 학생은 여러 과목을 수강할 수 있다.
- 한 교수는 한 과목만 강의할 수 있다.
- 한 과목은 여러 교수가 강의할 수 있다.
PK는 [학번, 과목]이고 함수 종속 관계는 [학번, 과목]→교수, 교수→과목이다.
왼쪽의 다이어그램에서 교수와 과목 간에 화살표가 사각형에 겹쳐 불완전하게 보인다. 따라서 강의 과목 릴레이션은 비록 3NF이지만 다음과 같은 문제점이 있다.
🏷 삽입 이상
교수 '김정희'가 '자료구조' 과목을 강의하게 되었을 때 삽입이 불가능하다. PK인 학번이 NULL이기 때문이다.
🏷 삭제 이상
학번 1234 학생이 '자료구조'를 취소할 때 '이우정'이 '자료구조'를 맡고 있는 정보까지도 삭제된다.
🏷 갱신 이상
교수 '김용주'의 강의 과목이 '데이터베이스'에서 '웹 프로그래밍'으로 변경되었을 때 '김용주'에 대한 모든 튜플에 대해 변경되어야만 한다.
이러한 이상 현상이 나타나는 이유는 강의 과목 릴레이션에서 키가 아닌 애트리뷰트가 다른 애트리뷰트를 결정하기 때문이다. 즉, 교수 애트리뷰트는 후보키가 아닌데 과목을 결정하는 결정자이다. 따라서 BCNF는 모든 결정자가 후보키가 되도록 분할하는 것이다.
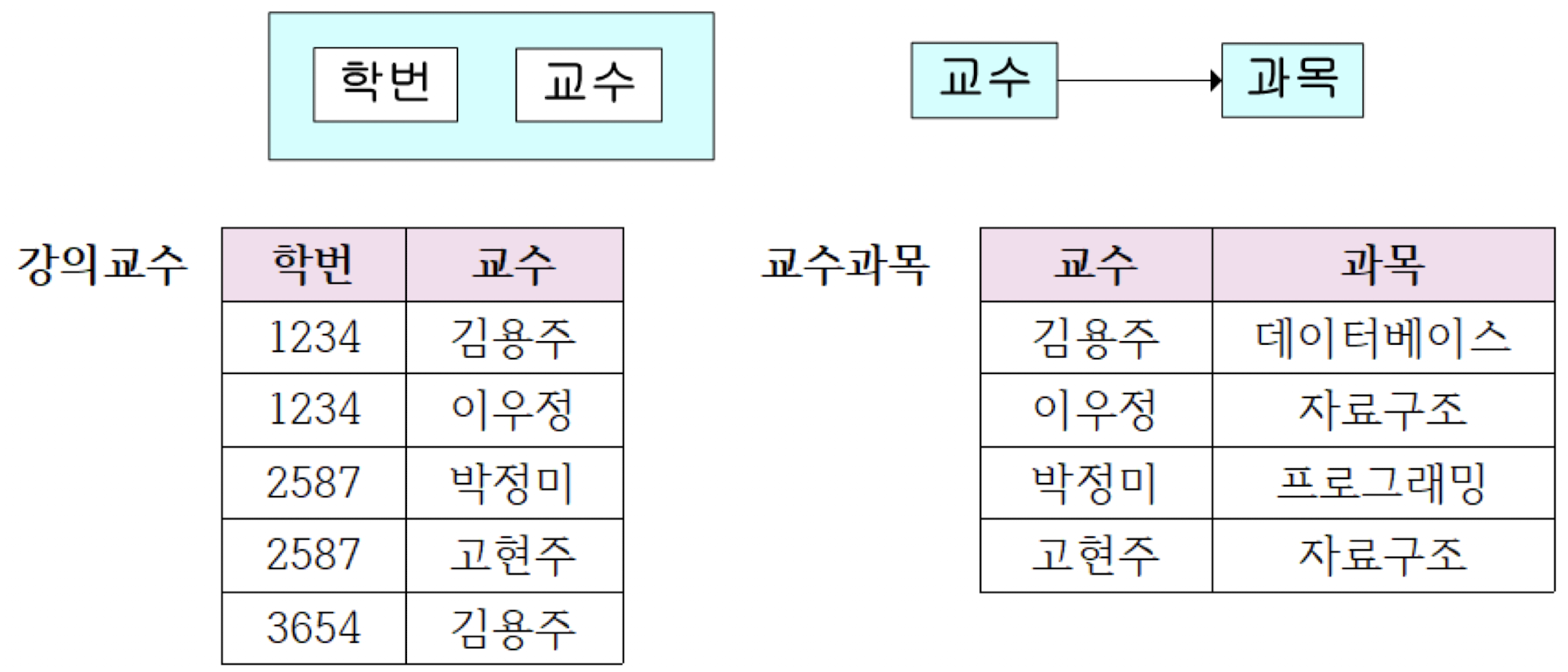
먼저 학번과 교수를 분리시키고, 교수가 키가 되도록 교수와 과목을 분리한다. 여기서 강의교수(학번, 교수)의 기본키는 [학번, 교수]이고 외래키인 [교수]는 교수과목 릴레이션의 교수를 참조한다. 그리고 교수과목(교수, 과목)의 기본키는 [교수]이다.
📂 제4 정규형
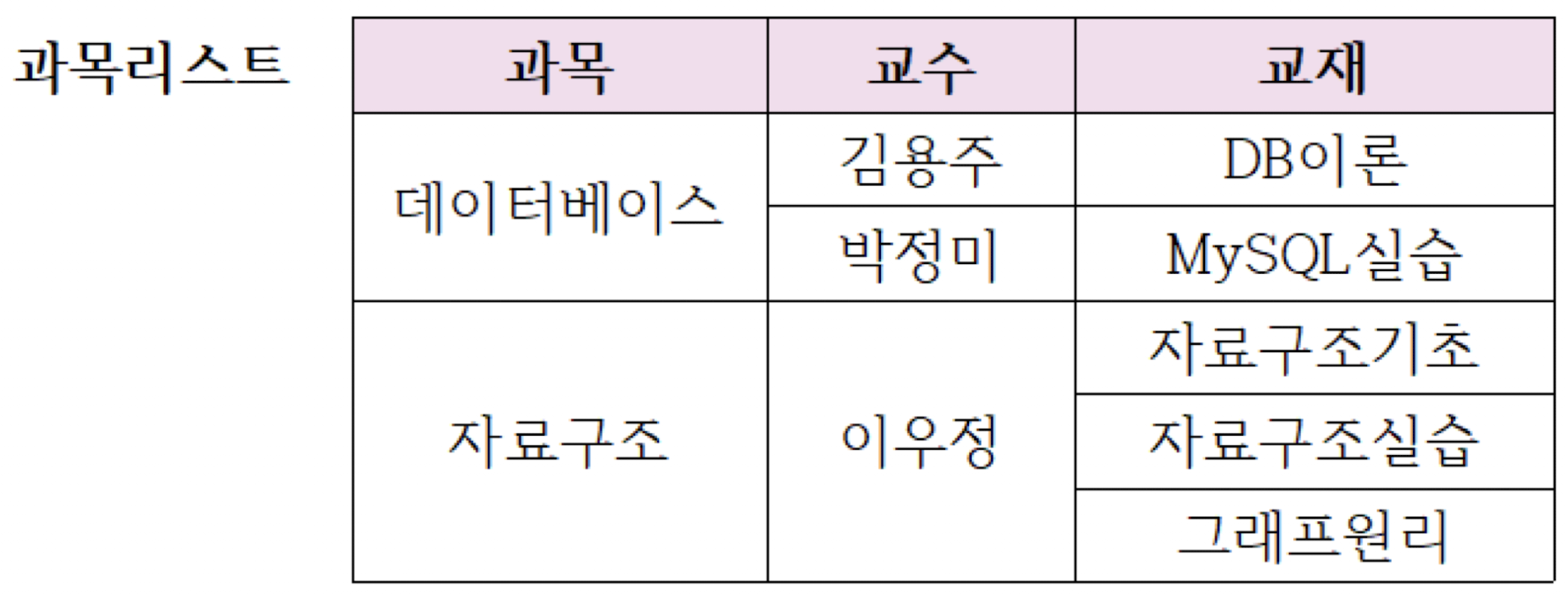
위 테이블은 비정규 릴레이션이다. 이 릴레이션에 대한 제약 조건은 "각 과목은 명시된 교수들 중에서 어떤 교수라도 가르칠 수 있으나, 교재는 기술된 것 전부 사용해야만 한다." 라고 제시된다. 이 비정규 릴레이션을 정규 릴레이션으로 변환시키면 아래와 같다.
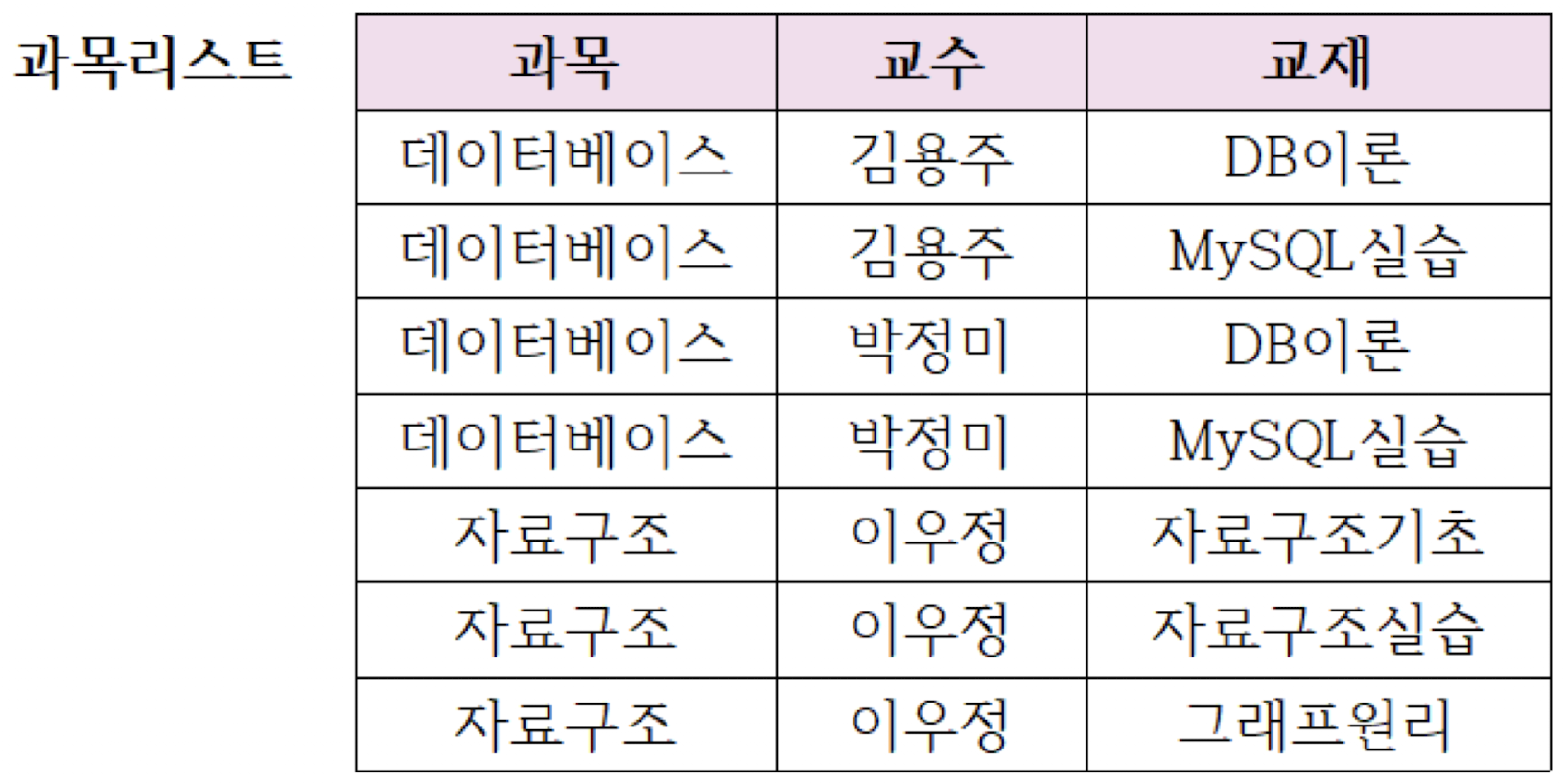
위 과목리스트 릴레이션은 모든 애트리뷰트 집합이 키가 되는 릴레이션이므로 자동적으로 BCNF가 된다. 그러나 이 릴레이션에서 한 과목은 여러 교수가 가르칠 수 있고, 또 여러 개의 교재를 가질 수 있다. 그리고 교수와 교재 사이에는 서로 직접적인 관련이 없다.
과목리스트 릴레이션에서 갱신 이상 현상을 살펴보자.
교수 '고현주'가 '자료구조'를 강의한다는 정보를 삽입하려면 3개의 자료구조 교재에 대해 각각 튜플 하나씩 3개의 튜플을 삽입해야 한다. 이는 상당한 데이터 중복이 발생되고 이런 중복은 당연히 바람직하지 않다.
이러한 BCNF 이상 현상의 이유는 과목은 교수나 교재의 값 하나를 결정하는 것이 아니라 몇 개의 값, 즉 값의 집합을 결정하기 때문이다. 이러한 형태의 종속을 다치 종속(MVD: Multi-valued Dependency)이라 하고 이를 표현할 때 '↠'로 표기한다.
과목리스트 릴레이션에서는 다음과 같은 두 개의 MVD를 가지고 있다.
과목 ↠ 교수
과목 ↠ 교재
예를 들어, 과목↠교수에서 '데이터베이스'는 값의 집합 [김용주, 박정미]와 대응하고, 과목↠교재에서는 [DB이론, MySQL실습]과 대응한다.
다치 종속은 튜플의 애트리뷰트가 집합 값을 허용하지 않는 제1 정규형으로 인하여 발생한다. 이를 해결하기 위해 제4 정규형(4NF) 릴레이션을 정의하자.
과목리스트 릴레이션을 다음과 같이 분해하자.

정리하면, 다치 종속(MVD)이란 릴레이션 R(A, B, C)에서 어떤 [A, C] 값에 대응되는 B 값의 집합이 A 값에만 종속되고 C 값에는 독립적이면, "B는 A에 다치 종속된다."라고 하고, A↠B로 표기한다. A↠B이면, A↠C도 성립한다. 이는 A↠B|C로도 표현될 수 있다.
📂제5 정규형
지금까지는 문제가 발생하면 두 개의 릴레이션으로 분해하였다. 하지만 어떤 릴레이션의 경우, 3개 또는 그 이상의 릴레이션으로 분해해야하는 경우가 있을 수 있다(n-분해 릴레이션).
다음의 예를 살펴보자.
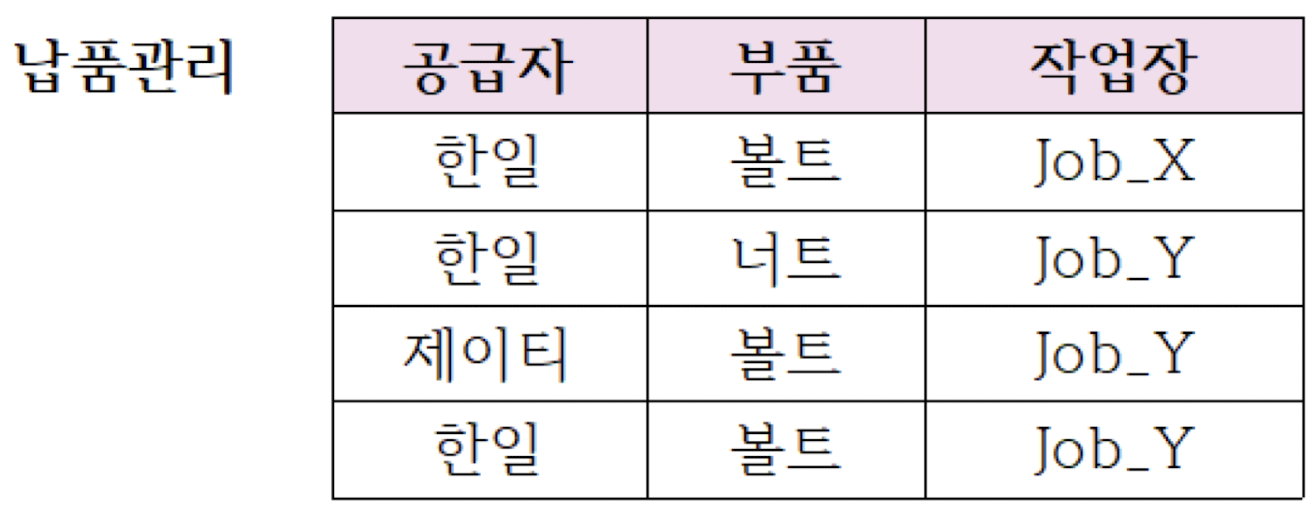
이 테이블에서 하나의 튜플은 어떤 공급자가 어떤 부품을 어떤 작업장에 공급하고 있다는 것을 내타내고 있다. 이 테이블은 모든 애트리뷰트의 집합이 키가 되고, 의미 있는 다치 종속이 존재하지 않으므로 이미 4NF에 속한다.
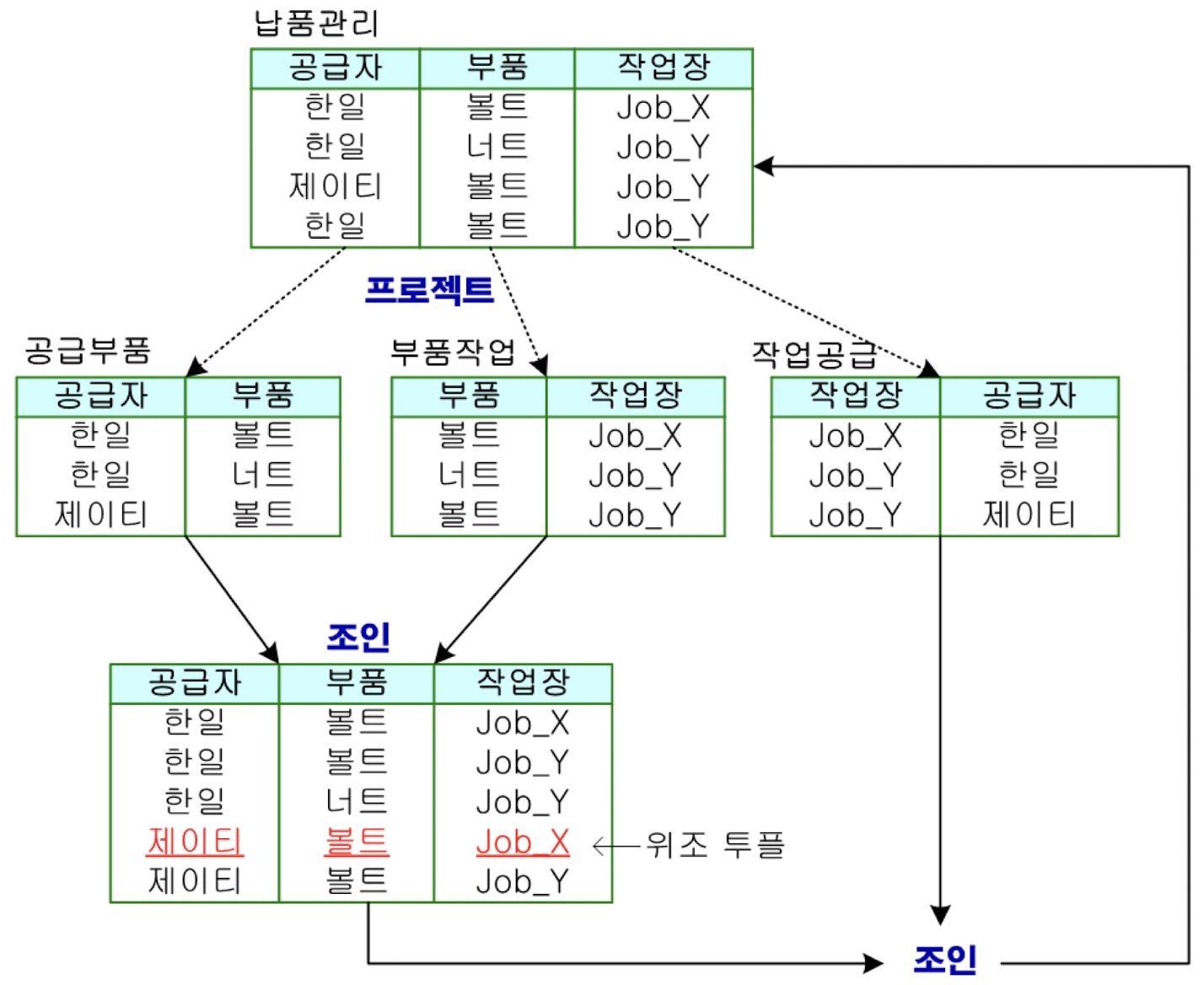
위의 릴레이션을 가지고 프로젝션으로 만든 3개의 릴레이션(공급부품, 부품작업, 작업공급)을 보여주고 있다. 또한 공급부품과 부품작업을 자연조인하고 그 결과를 다시 작업공급과 조인한 결과를 보여주고 있다.
여기서 유의할 점은 첫 번째 조인의 결과는 원래의 납품관리에는 없다 위조 튜플이 추가로 생성되어 있다가 두 번째 조인에서 제거되는 것이다.
이 같은 사실은 납품관리 릴레이션은 2개의 릴레이션으로 분해해서는 정보 무손실 분해가 되지 않고, 3개의 릴레이션으로 분해해야만 정보 무손실 분해가 될 수 있음을 보여준다. 이러한 제약 조건을 조인 종속(JD:Join Dependency)이라고 한다.
조인 종속이란, 어떤 릴레이션 R에 대해 프로젝트(∏)한 n개의 부분 집합(A,B,...Z)이 있다할 때, 이 때 만일 이 릴레이션 R이 그의 (A, B, ...Z)를 모두 조인한 결과와 똑같이 된다면 R은 조인 종속 (JD)*(A,B,...Z)을 만족시킨다고 한다.
하지만, 계속적인 분해로 인한 별다른 이점이 거의 없기 때문에 5NF는 현실적으로 잘 사용되지 않는다.
📂 정리
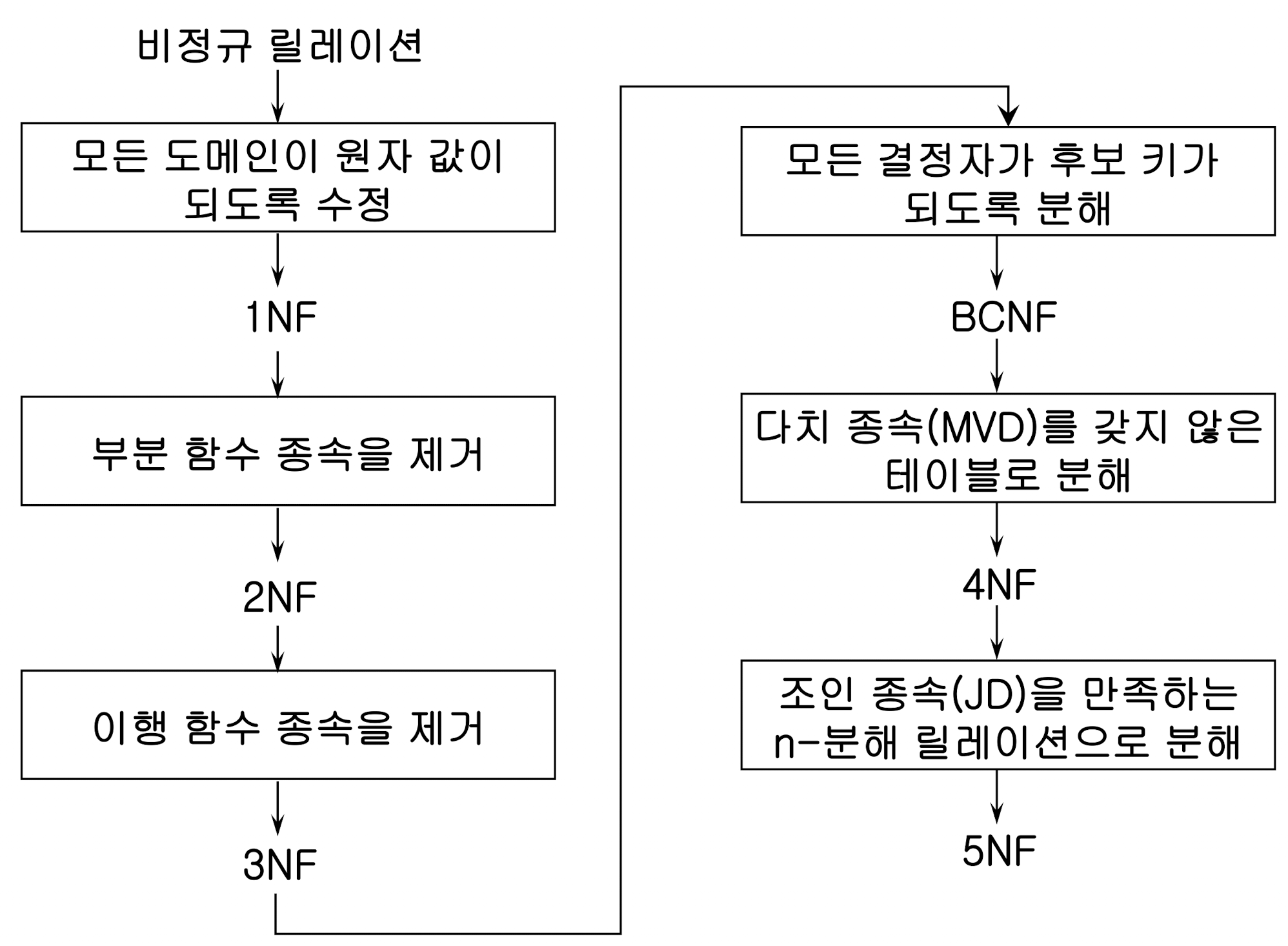
위의 모든 내용들을 정리하면 다음과 같다.
'데이터베이스' 카테고리의 다른 글
| [데이터베이스] 무결성, 보안 (0) | 2022.12.03 |
|---|---|
| [데이터베이스] 데이터베이스 설계 (1) | 2022.11.30 |
| [데이터베이스] SQL - 2 (0) | 2022.11.27 |
| [데이터베이스] SQL(Structured Query Language) - 1 (0) | 2022.11.26 |
| [데이터베이스] 데이터베이스 모델링 (0) | 2022.10.18 |


