문제 링크
https://www.acmicpc.net/problem/17387
17387번: 선분 교차 2
첫째 줄에 L1의 양 끝 점 x1, y1, x2, y2가, 둘째 줄에 L2의 양 끝 점 x3, y3, x4, y4가 주어진다.
www.acmicpc.net
💡 풀이
해당 문제는 CCW라는 기하 알고리즘을 사용합니다.
CCW
CCW는 Counter-ClockWise의 약어로
평면 위에 놓여진 세 점의 방향관계를 구하는 알고리즘
입니다.
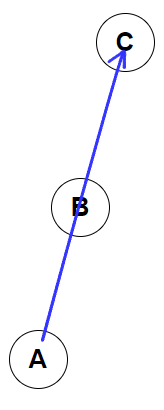
즉, CCW는 점 A, B, C를 순서대로 봤을 때, 부호에 따라 위치관계를 파악할 수 있습니다.
- CCW < 0 := 시계 방향
- CCW = 0 := 일직선
- CCW > 0 := 반시계 방향


CCW는 외적을 이용해서 계산합니다. 하지만, 여기서 CCW에 대해 자세하게 다루지는 않고, 계산하는 방법만 소개하겠습니다.
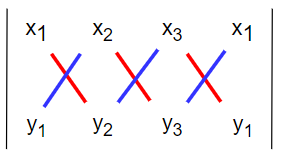
주어진 점 $A(x_1, y_1), B(x_2, y_2), C(x_3, y_3)$이 존재할 때, CCW는 다음과 같이 구할 수 있습니다.
$$CCW = (x_1y_2 + x_2y_3 + x_3y_1) - (y_1x_2 + y_2x_3 + y_3x_1)$$
그림으로 쉽게 설명해보면, 아래 그림에서 빨간 빗금을 각각 곱한 뒤 더해주고, 파란 빗금은 각각 곱한 뒤 모두 빼주면 됩니다.
문제 풀이
해당 문제에 이 CCW를 적용해봅시다. 점 A, B가 양 끝점인 선분 $L_1$과 점 C, D가 양 끝점인 $L_2$가 교차했는지 여부를 파악하는 문제입니다.
점 A, B를 기준으로 놓고 C와 D를 각각 확인해봤을 때, C와 D가 서로 반대 방향에 있어야 교차했다고 할 수 있습니다. 즉, 한 점이 시계 방향이면, 다른 하나는 반시계 방향이어야 합니다.
따라서, $CCW(A, B, C) * CCW(A, B, D)$와 $CCW(C, D, A)* CCW(C, D, B)$가 모두 음수라면 두 선분은 교차하고 있다고 말할 수 있습니다.
이제 둘 중 하나 혹은 두 값 다 0인 경우를 생각해봅시다.
우선, 하나만 0이라면 세 점이 동일 직선에 존재하는 경우이기 때문에 교차하는 것으로 판단합니다.
CCW 값이 둘 다 0인 경우는, 다음과 같이 두 가지 경우로 나뉘게 됩니다.

Case 1의 경우 교차가 아니고, Case 2의 경우만 교차로 판단해야 합니다.
따라서, 이와 같은 상황에서는 추가적인 조건이 필요합니다.
- A, B의 x 중 큰 값이 C, D의 x 중 작은 값보다 크거나 같아야 하고
- C, D의 x 중 큰 값이 A, B의 x 중 작은 값보다 크거나 같아야 한다.
- y 또한 성립해야 한다.
전체 코드
전체적인 코드는 다음과 같습니다.
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
class Q17387 {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st;
Point A, B, C, D;
st = new StringTokenizer(br.readLine());
A = new Point(Integer.parseInt(st.nextToken()), Integer.parseInt(st.nextToken()));
B = new Point(Integer.parseInt(st.nextToken()), Integer.parseInt(st.nextToken()));
st = new StringTokenizer(br.readLine());
C = new Point(Integer.parseInt(st.nextToken()), Integer.parseInt(st.nextToken()));
D = new Point(Integer.parseInt(st.nextToken()), Integer.parseInt(st.nextToken()));
int ccw1 = getCCW(A, B, C) * getCCW(A, B, D);
int ccw2 = getCCW(C, D, A) * getCCW(C, D, B);
// 둘 다 0인 경우
if (ccw1 == 0 && ccw2 == 0) {
if ((Math.max(A.x, B.x) >= Math.min(C.x, D.x) && Math.max(C.x, D.x) >= Math.min(A.x, B.x))
&& (Math.max(A.y, B.y) >= Math.min(C.y, D.y) && Math.max(C.y, D.y) >= Math.min(A.y, B.y))) {
System.out.println(1);
} else {
System.out.println(0);
}
} else if (ccw1 <= 0 && ccw2 <= 0) {
System.out.println(1);
} else {
System.out.println(0);
}
}
static int getCCW(Point p1, Point p2, Point p3) {
long result = (p1.x * p2.y + p2.x * p3.y + p3.x * p1.y) - (p1.y * p2.x + p2.y * p3.x + p3.y * p1.x);
return Long.compare(result, 0);
}
static class Point {
long y, x;
Point(long y, long x) {
this.y = y;
this.x = x;
}
}
}'알고리즘 > BOJ' 카테고리의 다른 글
| [BOJ] 14003 : 가장 긴 증가하는 부분 수열 5(Java) (1) | 2024.02.08 |
|---|---|
| [BOJ] 1509 : 팰린드롬 분할(Java) (1) | 2024.02.06 |
| [BOJ] 4386 : 별자리 만들기(Java) (0) | 2024.02.06 |
| [BOJ] 20303 : 할로윈의 양아치(Java) (1) | 2024.02.05 |
| [BOJ] 6603 : 로또(Java) (0) | 2024.01.31 |

