분할 정복(Divde & Conquer)은 가장 유명한 알고리즘 디자인 패러다임으로, 분할 정복 패러다임을 차용한 알고리즘들은
주어진 문제를 둘 이상의 부분 문제로 나운 뒤 각 문제에 대한 답을 재귀 호출을 이용해 계산하고,
각 부분 문제의 답으로부터 전체 문제의 답을 계산하는 것.
분할 정복 VS 일반적 재귀 호출
분할 정복이 일반적인 재귀 호출과 다른 점은 문제를 한 조각과 나머지 전체로 나누는 대신 거의 같은 크기의 부분 문제로 나눈다는 것이다. 아래의 두 그림이 이 둘의 차이점을 나타낸 그림이라 할 수 있다.
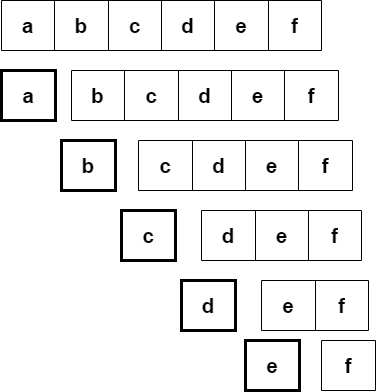
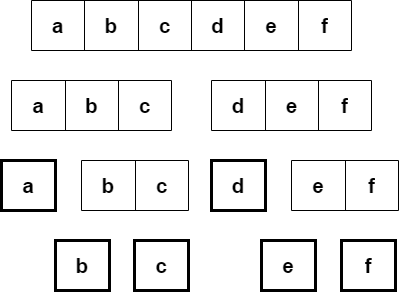
위의 그림은 항상 문제를 한 조각과 나머지로 쪼개는 일반적인 재귀 호출 알고리즘을 보여주고,
아래의 그림은 항상 문제를 절반씩으로 나누는 분할 정복 알고리즘을 보여준다.
분할 정복의 구성 요소
분할 정복을 사용하는 알고리즘들은 대게 세 가지의 구성 요소를 가지고 있다.
- 문제를 더 작은 문제로 분할하는 과정(divide)
- 각 문제에 대해 구한 답을 원래 문제에 대한 답으로 병합하는 과정(merge)
- 더이상 답을 분할하지 않고 곧장 문제를 풀 수 있는 매우 작은 문제(base case)
분할 정복을 적용해 문제를 해결하기 위해서는 문제에 몇 가지 특성이 성립해야 한다. 문제를 둘 이상의 부분 문제로 나누는 자연스러운 방법이 있어야 하며, 부분 문제의 답을 조합해 원래 문제의 답을 계산하는 효율적인 방법이 있어야 한다.
[예제 1] 수열의 빠른 합
$1+2+...+n$의 합을 찾는 분할 정복을 이용하는 $fastSum()$함수를 만들어 보자.
1부터 n까지의 합을 n개의 조각으로 나눈 뒤, 이들을 반으로 잘라 $n/2$개의 조각들로 만들어진 부분 문제 두 개를 만든다.(편의상 n은 짝수라 가정하자.)
$$fastSum() = 1+2+...+n = (1+2+...+n/2) + ( (n/2 + 1)+...+n)$$
첫 번째 부분 문제는 $fastSum(n/2)$로 나타낼 수 있지만, 두 번째 부분 문제는 그렇지 않다. 문제를 재귀적으로 풀기 위해서는 각 부분 문제를 '부터 n까지의 합' 꼴로 표현할 수 있어야 하는데, 위의 분할에서 두 번째 조각은 'a부터 b까지의 합' 형태를 가지고 있기 때문이다.
따라서 다음과 같이 두 번째 부분 문제를 $fastSum(x)$를 포함하는 형태로 바꿔 써야 한다.
$$(n/2+1)+...+n = (n/2+1) + (n/2+2) + ... + (n/2+n/2) = n/2 * n/2 + (1+2+3+...+n/2) = n/2*n/2+ fastSum(n/2)$$
공통된 항 n/2을 따로 빼내면 $fsatSum(n/2)$이 나타난다. 따라서 다음과 같이 쓸 수 있다.
$$fasfSum(n) = 2*fastSum(n/2) + n^2/4$$
단, 이는 n이 짝수일 경우이고, 홀수인 경우에는 짝수인 n-1까지의 합을 재귀 호출로 계산하고 n을 더해 답을 구한다.
[예제 2] 병합 정렬(Merge Sort)과 퀵 정렬(Quick Sort)
이 두 알고리즘은 모두 분할 정복 패러다임을 기반으로 해서 만들어진 것들이다. 이 알고리즘들의 직접적인 구현이나 증명보다는 그 동작 원리를 살펴보자.
병합 정렬 알고리즘은 주어진 수열을 가운데에서 쪼개 비슷한 크기의 수열 두 개로 만든 뒤 이들을 재귀 호출을 이용해 각각 정렬하는 것이다. 그 후 정렬된 배열을 하나로 합침으로써 정렬된 전체 수열을 얻는다.
반대로 퀵 정렬 알고리즘은 배열을 단순하게 가운데에서 쪼개는 대신, 병합 과정이 필요 없도록 한쪽의 배열에 포함된 수가 다른 쪽 배열의 수보다 항상 작도록 배열을 분할한다. 이를 위해 퀵 정렬은 파티션이라고 부르는 단계를 도입하는데, 이는 배열에 있는 수 중 임의의 '기준 수(pivot)'를 지정한 후 기준보다 작거나 같은 숫자를 왼쪽, 더 큰 숫자를 오른쪽으로 보내는 과정이다.
'알고리즘 > 알고리즘' 카테고리의 다른 글
| [Algorithm] 위상 정렬(Topological Sort) (0) | 2023.04.14 |
|---|---|
| [Algorithm] BFS : 너비 우선 탐색(Java) (0) | 2022.08.02 |
| [Algorithm] 플로이드-워셜(Floyd-Warshall) 알고리즘 (0) | 2022.07.06 |
| [Algorithm] 다익스트라(Dijkstra) 알고리즘 (1) | 2022.03.25 |

